Author(s): David Smith and Lang Moore                                                               Kembali

Pada bagian, kita akan menampilkan solusi dari model SIR melalui pendekatan solusi numerik, seperti Metode Euler yang sudah biasa kita gunakan. Namun demikian, kita tetap meninjau kembali gagasan dasar dari metode ini. 

Ingat kembali gagasan Metode Euler bahwa:

"Jika kita memiliki rumus slope/kemiringan," yaitu, cara untuk menghitung dy/dt pada sembarang titik (t, y), maka kita dapat menghasilkan barisan pada nilai y,

y0, y1, y2, y3, ...

dengan dimulai dari y0 yang diberikan dan menghitung setiap kenaikan sebagai kemiringan (slope). Artinya,

y_n = y_n-1 + slope_n-1*Delta_t

di mana Delta_t adalah ukuran langkah kecil yang sesuai dalam domain waktu.

Tidak jadi masalah dalam perhitungan ini jika rumus kemiringan yang terjadi tergantung tidak hanya pada variabel t dan y tetapi juga pada variabel lain. Katakanlah x dan z, selama kita tahu bagaimana hubungan x dan z dengan t dan y. Jika x dan z terjadi sebagai variabel dependen lain dalam sistem persamaan diferensial, maka kita dapat menghasilkan nilai x dan z dengan cara yang sama.

Tentu saja, untuk model SIR, kita ingin nama variabel dependen lainnya menjadi s, i, dan r. Dengan demikian kita memiliki tiga rumus Euler dalam bentuk

Untuk lebih jelas, kita ingat kembali model SIR,

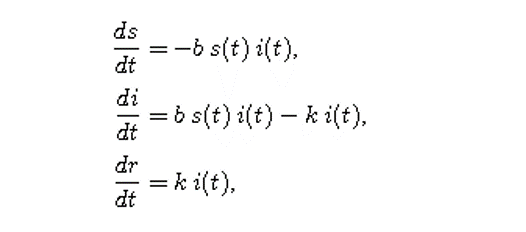
dalam formula Euler dapat dikonversi menjadi,

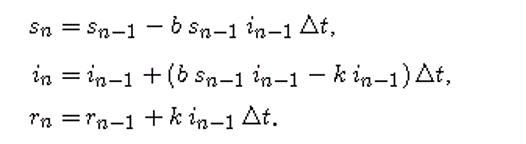
Tentu saja, untuk menghitung sesuatu dari rumus ini, kita harus memiliki nilai eksplisit untuk b, k, s(0), i(0), r(0), dan Delta_t. Pada bagian ini kami mengeksplorasi kecukupan formula ini untuk menghasilkan solusi dari model SIR. Jika ada aplikasi yang memiliki Metode Euler sebagai pilihan, kita boleh menggunakannya daripada harus mengonstruksi rumus dari awal.

1. Pada lembar kerja aplikasi yang anda gunakan, terdapat perintah untuk menemukan solusi persamaan diferensial. Gunakan perintah ini, dengan nilai sampel b = 1/2 dan k = 1/3, untuk menghasilkan solusi grafis dari persamaan SIR, mulai dari s(0) = 1, i(0) = 1.27e-6, dan r(0) = 0.
2. Sekarang bangkitkan solusi Metode Euler untuk tiga sektor populasi. Mulai dengan ukuran langkah yang relatif kasar Delta_t = 10 hari, dan biarkan rentang t hingga 150 hari. Sesuaikan solusi ini pada solusi "exact" Langkah 1. Menurut anda, apakah Metode Euler dapat digunakan untuk memprediksi solusi yang tepat dari sistem? Mengapa atau mengapa tidak? Apa karakteristik Metode Euler yang menyebabkan prediksi solusi berperilaku seperti itu?
3. Ubah ukuran langkah menjadi 1 hari dan plot kembali solusi Metode Euler. Sekarang apakah hal ini dapat memprediksi solusi yang tepat dari sistem? Mengapa atau mengapa tidak?
4. Temukan ukuran langkah yang tepat pada Metode Euler untuk memprediksi solusi yang tepat dari sistem.

Link Artikel

• Model SIR untuk Penyebaran Penyakit - Latar Belakang
• Model SIR untuk Penyebaran Penyakit - Model Persamaan Diferensial
• Model SIR untuk Penyebaran Penyakit - Metode Euler
• Model SIR untuk Penyebaran Penyakit - Hubungan Parameter dengan Data
• Model SIR untuk Penyebaran Penyakit - Jumlah Kontak
• Model SIR untuk Penyebaran Penyakit - Kekebalan
• Model SIR untuk Penyebaran Penyakit - Ringkasan