Author(s): David Smith and Lang Moore                                                               Kembali

Rata-rata periode infeksi untuk Flu Hong Kong diketahui sekitar tiga hari, sehingga estimasi k = 1/3 yang kita gunakan mungkin tidak terlalu jauh. Adapun estimasi b yang kita gunakan hanyalah tebakan. Lebih lanjut, perkiraan yang baik tentang "laju kontak" populasi pasti akan tergantung pada banyak karakteristik populasi, seperti tingkat kepadatan penduduk. Pada bagian ini, kita akan melakukan ujicoba efek parameter pada solusi, lalu mencoba untuk menemukan nilai yang sesuai dengan data kematian yang terjadi di New York City. Kita fokuskan percobaan pada kelompok individu terinfeksi, i(t), karena kelompok ini memberikan informasi terkait perkembangan penularan penyakit.

1. Percobaan pertama kita lakukan dengan perubahan pada nilai parameter b dengan nilai k tetap 1/3. Plot grafik i(t) dengan beberapa nilai b antara 0,5 dan 2,0. Jelaskan bagaimana efek perubahan b ini terhadap grafik i(t). Tetap waspada untuk perubahan otomatis pada skala vertikal. Untuk memudahkan pengamatan, variasikan warna dan overlay grafik secara berurutan.
2. Jelaskan secara singkat mengapa perubahan yang terjadi pada model epidemi dapat diterima secara intuitif.
3. Selanjutnya lakukan percobaan dengan perubahan pada nilai k. Kembali gunakan b=1/2 dengan perubahan nilai k yang berbeda pada rentang 0,1 dan 0,6. Jelaskan perubahan yang terjadi pada grafik i(t). Kembali waspada untuk perubahan otomatis pada skala vertikal. Untuk memudahkan pengamatan, variasikan warna dan overlay grafik secara berurutan.
4. Jelaskan perubahan yang terjadi pada model sesuai dengan pemahaman anda secara intuitif.
5. Perhatikan bahwa terdapat perubahan karakter grafik i(t) pada rentang nilai k yang digunakan (0,1 - 0,6). Perubahan apa yang terjadi dan di mana hal itu terjadi?
6. Gunakan persamaan diferensial proporsi individu terinfeksi untuk menjelaskan bagaimana dapat memperkirakan nilai k dimana karakter grafik i(t) berubah.
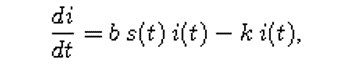
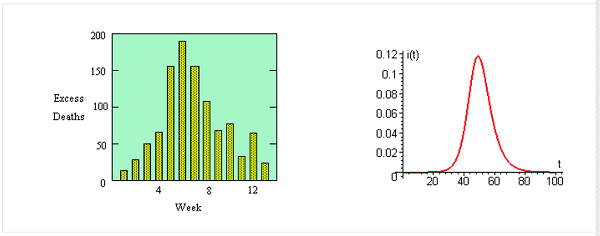
7. Sekarang kita bandingkan model dengan data. Ingat bahwa ini adalah jumlah kematian setiap minggu yang dapat dikaitkan dengan kasus epidemi flu. Jika kita berasumsi bahwa proporsi kematian di antara individu terinfeksi adalah konstan, maka jumlah kematian per minggu secara kasar harus sebanding dengan jumlah orang yang terinfeksi pada beberapa minggu sebelumnya. Perhatikan kembali grafik data dan grafik i(t) dengan nilai k = 1/3 dan b = 6/10. Apakah model itu tampak masuk akal atau tidak? Jelaskan kesimpulan Anda.

Link Artikel

• Model SIR untuk Penyebaran Penyakit - Latar Belakang
• Model SIR untuk Penyebaran Penyakit - Model Persaman Diferensial
• Model SIR untuk Penyebaran Penyakit - Metode Euler
• Model SIR untuk Penyebaran Penyakit - Hubungan Parameter dengan Data
• Model SIR untuk Penyebaran Penyakit - Jumlah Kontak
• Model SIR untuk Penyebaran Penyakit - Kekebalan
• Model SIR untuk Penyebaran Penyakit - Ringkasan