Author(s): David Smith and Lang Moore                                                               Kembali

Setiap strain flu memberi kekebalan di masa yang akan datang bagi pengidapnya. Untuk penyakit seperti ini, jika hampir semua orang mengalaminya, maka mereka yang belum mengalami akan terlindung dari darinya sehingga tidak cukup suseptibilitas tersisa di populasi untuk memungkinkan epidemi terjadi. Perlindungan seperti ini disebut kekebalan kelompok.

Pada Bagian 3 kita bereksperimen dengan ukuran relatif pada b dan k, dan kita temukan bahwa, jika b lebih kecil dari k, maka tidak ada epidemi yang dapat berkembang. Kemudian pada Bagian 4, jika jumlah kontak c = b/k cukup kecil, maka tidak akan ada kasus epidemi. Namun cara lain untuk mencegah terjadinya epidemi adalah dengan mengurangi populasi pada individu rentan secara artifisial dengan inokulasi.

Inti dari inokulasi adalah menciptakan kekebalan kelompok dengan merangsang antibody sebanyak mungkin yang dapat memberikan kekebalan. Dengan demikian inokulasi menciptakan jalur langsung dari kelompok individu rentan ke kelompok individu yang pulih tanpa melewati kelompok terinfeksi (lihat diagram di bawah). Dan program inokulasi berskala besar untuk mencegah epidemi yang akan datang cukup cepat untuk menurunkan populasi rentan ke tingkat yang aman sehingga jika tingkat infeksi masuk ke populasi, beberapa orang mungkin sakit, namun tidak ada epidemi yang akan berkembang.

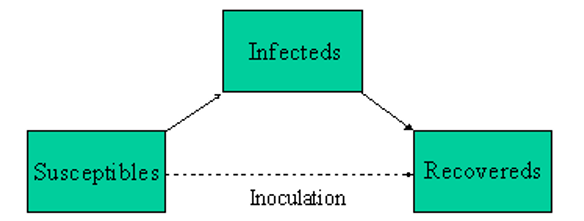
Jadi, berapa proporsi penduduk yang harus diinokulasi untuk mendapatkan kekebalan kelompok? Atau, dengan kata lain, seberapa kecil s0 yang harus dipenuhi untuk memastikan bahwa epidemi tidak dapat dimulai? Itu tergantung pada jumlah kontak.

1. Mengontrol terjadinya kasus epidemi sama dengan menjaga di/dt tetap negatif dari  t = 0 dan seterusnya, mengapa demikian?

2. Tulis ruas kanan dari persamaan diferensial proporsi individu terinfeksi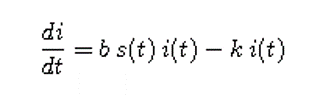

Jelaskan mengapa salah satu faktor selalu positif dan mengapa tanda faktor lain tergantung pada s (t)?

3. Jelaskan mengapa s(t) merupakan fungsi turun, sehingga memiliki nilai terbesar pada t=0. Hal ini berakibat, jika di/dt negatif pada waktu 0, maka ia tetap negatif.

4. Tunjukkan bahwa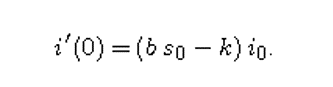

Jelaskan mengapa, jika s0 kurang dari 1/c, maka tidak ada epidemi yang bisa berkembang.

5. Dari tahun 1912 hingga 1928, jumlah kontak untuk kasus campak di AS adalah 12,8. Jika kita berasumsi bahwa c masih 12,8 dan inokulasi 100% efektif (setiap orang yang diinokulasi memperoleh kekebalan dari penyakit), berapa proporsi populasi yang harus diinokulasi untuk mencegah epidemi?

6. Anggaplah vaksin hanya 95% efektif. Berapa proporsi penduduk harus diinokulasi untuk mencegah epidemi campak?

Link Artikel

• Model SIR untuk Penyebaran Penyakit - Latar Belakang
• Model SIR untuk Penyebaran Penyakit - Model Persamaan Diferensial
• Model SIR untuk Penyebaran Penyakit - Metode Euler
• Model SIR untuk Penyebaran Penyakit - Hubungan Parameter dengan Data
• Model SIR untuk Penyebaran Penyakit - Jumlah Kontak
• Model SIR untuk Penyebaran Penyakit - Kekebalan
• Model SIR untuk Penyebaran Penyakit - Ringkasan