Model SIR untuk Penyebaran Penyakit - Jumlah Kontak
Author(s): David Smith and Lang Moore Kembali
Pada Bagian sebelumnya kita anggap parameter b dan k dapat diperkirakan, sehingga dimungkinkan untuk menghasilkan solusi numerik dari persamaan diferensial. Bahkan, seperti yang telah kita lihat, proporsi k yang pulih dari infeksi pada hari tertentu dapat diperkirakan melalui pengamatan pada individu terinfeksi. Secara khusus, k kurang lebih adalah kebalikan dari jumlah hari yang dibutuhkan bagi individu yang sakit untuk dapat menginfeksi orang lain. Pada sebagian besar penyakit menular, waktu infeksi diperkirakan sama untuk kebanyakan orang terinfeksi dan dikenal melalui observasi.
Pada bagian ini kita akan melihat cara tak langsung untuk mengamati parameter b. Pertimbangkan rasio dari b ke k :
| b/k | = b x 1/k |
| = jumlah kontak tertutup per hari per infeksi x jumlah hari infeksi | |
| = jumlah kontak tertutup per individu terinfeksi. |
Rasio ini kita sebut jumlah kontak, ditulis c = b/k. Jumlah kontak c adalah karakteristik gabungan dari populasi dan penyakit. Pada populasi yang sama, ia mengukur penularan penyakit yang relatif, karena memberitahu kita secara tidak langsung berapa banyak kontak yang cukup dekat untuk benar-benar menyebarkan penyakit. Kalkulus dapat kita gunakan untuk menunjukkan bahwa c dapat diperkirakan setelah proses epidemi berlangsung. Dengan demikian b dapat dihitung sebagai c k.
Kembali kita lihat persamaan diferensial untuk s dan i sebagai berikut:
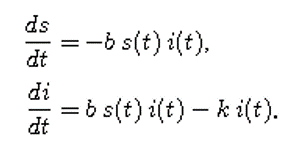
Kita dapat menghasilkan bentuk yang lebih sederhana dari kedua persamaan dengan membagi persamaan kedua dengan persamaan pertama - dengan catatan kita dapat memahami arti pada ruas kiri.
1. Gunakan aturan rantai untuk menjelaskan kenapa diperoleh bentuk:
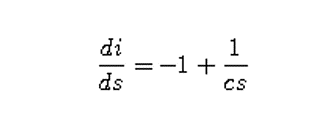
Persamaan diferensial pada langkah 1 menentukan (kecuali untuk ketergantungan pada kondisi awal) proporsi yang terinfeksi i sebagai fungsi dari proporsi rentan s. Kita akan menggunakan solusi dari persamaan diferensial ini untuk dua kondisi awal khusus, untuk menggambarkan cara menentukan jumlah kontak.
Tiga bagian dari persamaan diferensial baru ini penting untuk diperhatikan:
- Satu-satunya parameter yang muncul adalah c.
- Persamaannya tidak bergantung pada waktu. Artinya, apa pun yang kita pelajari tentang hubungan antara i dan s berlaku untuk seluruh durasi epidemi.
- Ruas kanan adalah fungsi eksplisit dari s, yang sekarang menjadi variabel independen.
2. Tunjukkan bahwa i(s) berbentuk:
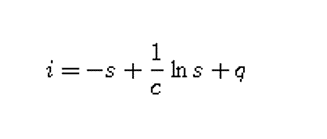
dimana q adalah konstanta.
3. Jelaskan mengapa
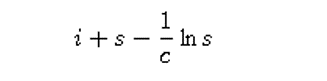
harus bebas dari waktu.
Kita dapat mengetahui (atau dapat memperkirakan) nilai-nilai i dan s sebanyak 2 kali, yaitu pada t = 0 dan t = tak hingga. Untuk penyakit seperti flu Hong Kong, i(0) sekitar 0 dan s(0) sekitar 1. Setelah proses epidemi berlangsung lama, kita memilikidapat i(tak hingga) kembali ke sekitar 0, dan s(tak hingga) berada pada nilai titik tetapnya. Jika ada pelaporan yang baik dari jumlah kasus yang terinfeksi penyakit, maka titik tetap dapat diamati sebagai proporsi populasi yang bebas penyakit.
4. Untuk kasus epidemi semacam itu, jelaskan mengapa
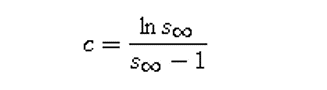
[Petunjuk: Gunakan fakta bahwa kuantitas pada langkah 3 sama pada saat t = 0 dan t = tak hingga].
5. Gunakan salah satu solusi numerik pada sub bab sebelumnya untuk memperkirakan nilai s(tak hingga). Gunakan nilai ini untuk menghitung jumlah kontak c untuk kasus flu Hong Kong lalu bandingkan hasilnya dengan nilai yang dihitung berdasarkan definisi, c = b/k.
Link Artikel
- Model SIR untuk Penyebaran Penyakit - Latar Belakang
- Model SIR untuk Penyebaran Penyakit - Model Persamaan Diferensial
- Model SIR untuk Penyebaran Penyakit - Metode Euler
- Model SIR untuk Penyebaran Penyakit - Hubungan Parameter dengan Data
- Model SIR untuk Penyebaran Penyakit - Jumlah Kontak
- Model SIR untuk Penyebaran Penyakit - Kekebalan
- Model SIR untuk Penyebaran Penyakit - Ringkasan
Kategori
Arsip
- July 2023 (3)
- January 2023 (1)
- December 2022 (1)
- August 2022 (1)
- July 2022 (6)
- March 2022 (1)
- September 2021 (2)
- October 2020 (1)
- July 2020 (2)
- April 2020 (1)
- November 2019 (1)
- September 2019 (1)
- August 2019 (2)
- July 2019 (1)
- May 2019 (1)
- February 2019 (1)
- September 2018 (2)
- August 2018 (1)
- July 2018 (4)
- June 2018 (5)
- September 2017 (2)
- August 2017 (1)
- April 2017 (1)
- October 2016 (1)
- September 2016 (2)
- September 2015 (4)
- June 2015 (1)
Blogroll
- 01 Sistem Informasi Akademik
- 02 Repository UNG
- 03 Universitas Negeri Gorontalo
- 04 Beasiswa DIKTI
- 05 Beasiswa LPDP
- 06 BookFi
- 07 Indonesian Mathematical Society
- 08 EBSCOhost
- 09 Library Genesis
- 10 Khan Academy
- 11 Blog Pribadi
- 12 Twitter
- 13 Facebook
- 14 Pdf Drive
- 15 Pangkalan Data UNG
- 16 Differential Equation
- 17 Math is Fun
- 18 Jambura Journal of Mathematics
- 19 OSF
- 20 Sci-Hub
- 21 Researchsquare
- 22 Kalkulator Math
- 23 Gometa
- 24 Microsite
- 25 Wordwall
- 26 Science Direct
- 27 BSRE BSSN
- 28 OpenAI
- 29 Quillbot
- 30 Perplexity
- 31 Citation FInder
