Bagi para peneleti terutama dosen baik PTN maupun PTS di Indonesia, saat ini diwajibkan untuk memiliki akun di sinta.kemdikbud.go.id karena seluruh data tridharma dosen akan terekam diakun sinta yang selanjutnya diakumulasi menjadi skor sinta untuk pemeringkatan author maupun institusi peneliti/dosen. Bagai peneliti/dosen yang belum memiliki akun sinta, disarankan untuk segera registrasi melalui portal sinta.kemdikbud.go.id.

Cara registrasi akun sinta dan sinkronisasi data

Ketika pertama kali membuat akun, biasanya keterangan institusi/program studi/homebase dosen tidak secara otomatis terbaca di profil sinta, melainkan akan terbaca UNKNOWN. Jika tidak segera diupdate, maka data dosen beserta seluruh kinerjanya dalam bentuk skor SINTA tidak akan terbaca sehingga tidak berdampak pada peringkat institusi/homebasenya. Untuk itu, dosen perlu melalukan sinkronisasi/update data program studi dengan langkah-langkah sebagai berikut:

1. Login dengan menggunakan Email dan Password yang digunakan saat registrasi sinta.
2. Arahkan kursor ke Nama lalu Klik My Profile.
3. Arahkan kursor ke SINTA ID dibagian pojok kanan atas lalu klik Update Profile.
4. Klik kotak Sync PDDIKTI pada bagian SINTA Profile, maka akan muncul notifikasi Success! Sync PDDIKTI Success.
5. Terakhir klik kotak Update Profile di bagian bawah, maka masalah Program Studi yang tidak terbaca sudah teratasi.

Demikian cara update data Program Studi pada Profil Dosen di SINTA Kemdikbud, semoga bermanfaat.

Jika pada tulisan sebelumnya dibahas Cara Mudah Membuat Akun di Google Scholar dan Cara merger ID Garuda, maka pada tulisan kali ini kita akan bahas bagaimana cara membuat akun SINTA dan bagaimana menautkannya dengan profil publikasi seperti Scopus, Web of Science, Garuda, dan Google Scholar. Sebagaimana telah diketahui bahwa akun SINTA menjadi sesuatu yang wajib untuk dimiliki oleh setiap dosen saat ini, karena rekam jejak setiap dosen akan dilihat dan dinilai berdasarkan profil SINTA yang dimiliki. Dalam hal ini, klasterisasi perguruan tinggi juga akan dinilai berdasarkan rekam jejak dan kinerja dosennya yang tercantum di SINTA. Semakin banyak karya dosen yang terindeks di SINTA, akan semakin bagus posisi Institusinya dalam klasterisasi Perguruan Tinggi.

Oleh karena itu, berikut kita bahas bagaimana cara membuat akun di SINTA. Apa saja yang perlu disiapkan untuk membuat akun SINTA? Pada prinsipnya tidak perlu ada persiapan khusus, yang wajib ada adalah Akun Google Scholar, NIK dan Email (disarankan menggunakan email dengan domain institusi). Selanjutnya, anda hanya perlu mengingat NIDN atau NIDK bagi dosen PTS.

Berikut langkah-langkah untuk membuat akun SINTA dan menautkan akun scholar dan scopus ke SINTA:

1. Buka Browser dan masukan URL https://sinta.kemdikbud.go.id/logins/registration.                  
2. Pilih salah satu Status Author (Lecturer, Researcher atau Foreign Lecturer/Researcher)
3. Jika anda seorang dosen, maka pilih Lecturer lalu masukkan NIDN/NIDK pada kolom disebelah kanannya.
4. Pilih negara (Indonesia tentunya), masukkan nama lengkap (tanpa gelar akademik), ketikkan nama Institusi lalu pilihlah data institusi yang benar yang muncul pada autocomplete.                                                                                           
5. Pilih Academic Grade (Jabatan Fungsional) yang sesuai, masukukkan NIK pada kolom ID Card Number.
6. Masukkan email anda, lalu buat Password yang aman dan mudah diingat pada kolom yang sesuai.   
7. Klik tombol Registration untuk memproses data.
8. Selanjutnya perlu dilakukan aktivasi akun SINTA. Silahkan cek pesan masuk pada email dan klik link aktivasi dari SINTA. Jika tidak menemukan di kotak masuk, bisa cek pada bagian spam.
9. Setelah proses aktivasi maka pendaftar akan mendapatkan email pemberitahuan bahwa akun sudah teraktivasi.
10. Setelah ini, anda dapat login dengan email dan password yang sudah dibuat pada saat registrasi.
11. Langkah terakhir, silahkan menghubungi verifikator SINTA Institusi anda untuk melakukan verifikasi pada akun SINTA anda.

Demikian cara registrasi akun SINTA dan menautkan akun Google Scholar dan Scopus ke SINTA. Setelah dilakukan registrasi, perlu dilakukan sinkronisasi data dari profil publikasi seperti Scopus, Web of Science, Garuda, dan Google Scholar. Untuk proses ini dapat dilakukan dengan dengan mengikuti langkah-langkah sebagai berikut:

1. Silahkan login pada https://sinta.kemdikbud.go.id/ menggunakan email dan password yang telah dibuat sebelumnya.
2. Klik My Profile pada nama anda dibagian pojok kanan atas.
3. Klik Sinta ID lalu pilih Update Profile pada pojok kanan atas, maka muncul tampilan seperti pada Gambar berikut:
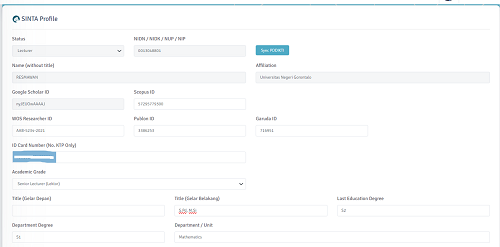
4. Klik Sync PDDIKTI untuk menyesuaikan dengan Data pada PDDIKTI, lalu masukkan ID Scopus, ID Garuda, ID Publon, dan ID WoS pada kolom yang bersesuaian.
5. Langkah terakhir, klik Update Profile pada bagian kiri bawah.
6. Langkah berikut, silahkan lakukan sinkronisasi data scopus, WoS, Garuda, dan Scholar pada menu My SINTA (Sidebar bagian Kiri). Perlu diingat bahwa permintaan sinkronisasi data hanya dapat dilakukan sekali dalam 7 hari.
7. Data lain seperti buku ber ISBN dan HAKI dapat ditambahkan secara manual, namun selanjutnya membutuhkan verifikasi dari operator SINTA Perguruan Tinggi.

Demikian cara Cara Registrasi Akun SINTA bagi Dosen atau Peneliti serta Sinkronisasi Data Scopus, WoS, garuda, dan Google Scholar. Semoga bermanfaat.

Kepada seluruh calon mahasiswa baru Universitas Negeri Gorontalo Tahun Akademik 2022-2023, pastikan untuk mendapatkan informasi PKKMB (Pengenalan Kehidupan Kampus Mahasiswa Baru) hanya dari akun resmi Universitas Negeri Gorontalo.

Info PKKM UNG 2022-2023

Bagi dosen atau peneliti, ID Garuda termasuk salah satu diantara sekian banyak identitas yang diperlukan untuk mencatat rekam jejak kinerja di bidang penelitian. ID Garuda adalah salah satu ID yang perlu di input dan disnkronkan ke Profil SINTA Kemdikbud untuk merekam seluruh publikasi hasil penelitian yang pernah dilakukan oleh seorang dosen atau peneliti. Namun demikian, bagi dosen atau peneliti yang telah menerbitkan beberapa publikasi yang terindeks di Garuda, terkadang juga terekam beberapa ID karena adanya perbedaan metadata yang dinput oleh pengelola jurnal. Oleh karena itu, perlu dilkaukan proses MERGER untuk mendapatkan satu ID tetap yang akan disinkronkan dengan Profil SINTA. Berikut langkah-langkah yang harus dilakukan untuk merger ID garuda:

1. Silahkan kunjungi portal garuda di laman https://garuda.kemdikbud.go.id/
2. Pilih Advanced Search, pilih authors, lalu ketikkan nama anda pada kolom Author Name.
3. Setelah itu klik Search, maka muncul semua nama yang terekam dengan ID berbeda di Garuda.
4. Jika terekam banyak nama dengan ID berbeda, silahkan perluas halaman pencarian jadi 100 per page agar semua nama bisa terlihat sekaligus.
5. Silahkan centang semua nama anda lalu klik Merge Authors Request pada bagian bawah.
6. Setelah itu akan terekam semua format Nama Author, ID, Afiliasi, dan judul artikel yang telah terekam di portal Garuda. Silahkan anda pilih ID, Nama, dan Afiliasi yang diinginkan sebagai identitas akhir setelah Merger. Masukkan email aktif yang anda gunakan sebagai email korespondensi. Jika muncul judul artikel yang bukan publikasi anda, silahkan hilangkan centangnya.
7. Klik Send Request, maka proses merger selesai. 

Admin Garuda membutuhkan waktu 14 hari kerja untuk menyelesaikan permintaan anda, namun terkadang bisa selesai lebih cepat. Silahkan cek secara berkala ID anda, dan jangan lupa untuk memasukkan ID Garuda pada profil SINTA.

Demikian cara merger ID Garuda bagi dosen atau Peneliti yang memiliki beberapa ID di Portal Garuda. Semoga bermanfaat.

Tulisan ini adalah tutorial yang ditujukan bagi penulis yang hendak menyerahkan/submit naskah pada jurnal ilmiah berbasis OJS (Open Journal System) 2. Sebagai informasi bahwa saat ini pengelola jurnal umumnya menggunakan dua jenis platform OJS dalam tata kelola jurnal yaitu, OJS versi 2 dan OJS versi 3 yang sedikit ada perbedaan dalam manajemennya. Penyerahan naskah melalui OJS pada prinsipnya sangat mudah, namun terkadang banyak author yang melewatkan beberapa hal yang dianggap sepele tapi sebenarnya penting. Hal ini meskipun sepele namun terkadang bisa berakibat proses submisi yang dilakukan tidak sempurna dan bahkan dapat mempengaruhi respon editor jurnal dalam menerima naskah. Berikut adalah tutorial Penyerahan Naskah pada Jurnal Ilmiah berbasis OJS 2:

1. Sebelum melakukan proses submission, pastikan sudah punya akun untuk login di jurnal yang dituju. Baca cara registrasi akun menggunakan OJS 2 disni.
2. Pastikan naskah yang akan disubmit sudah ditulis sesuai Author Guidelines dan template jurnal yang dituju.
3. Setelah poin 1 dan 2 selesai, silahkan login pada jurnal tujuan, maka akan tampil menu user pada gambar berikut 
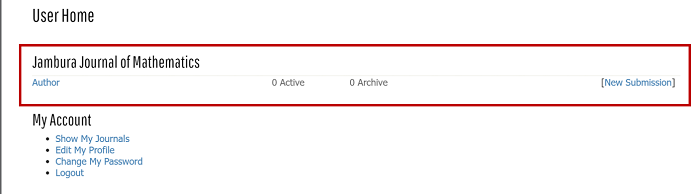
4. Langkah selanjutnya, klik New Submission, maka akan muncul tampilan berikut: Pada tahapan ini, author wajib untuk membaca semua informasi yang ditampilkan dan wajib centang semua kotak checklist yang tersedia.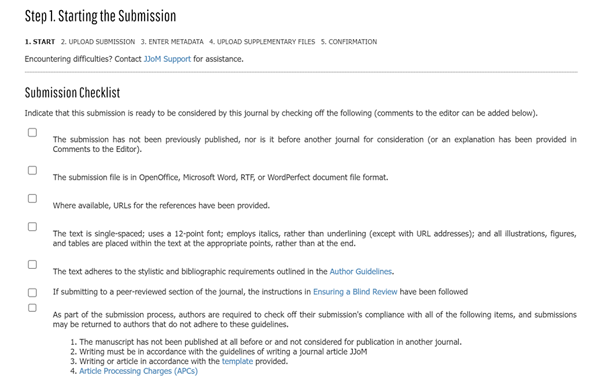
5. Pada bagian bawah langkah 4 akan tampil kotak "Comments for the Editor" yang sifatnya optional. Bagian ini yang terkadang dilewatkan oleh author karena sifatnya optional, padahal isian pada kotak ini bisa jadi sangat berpengaruh terhadap keputusan editor dalam menangani naskah telah diserahkan oleh author. Pada isian ini, sangat dianjurkan bagi author untuk memberikan pengantar pada editor berisi informasi tentang topik penting yang dibahas dalam penelitian, lalu menjelaskan secara singkat kenapa naskah yang diserahkan layak untuk diproses penerbitannya. Jika author menjelaskan dengan baik, bisa jadi editor akan langsung menyambut dan memperoses penerbitan naskah tanpa menunggu waktu yang lama, namun jika author tidak mengisi apapun pada kotak ini, maka editor tidak punya alasan untuk langsung melihat naskah yang telah diserahkan, telebih jika sudah banyak naskah yang telah disubmit sebelumnya.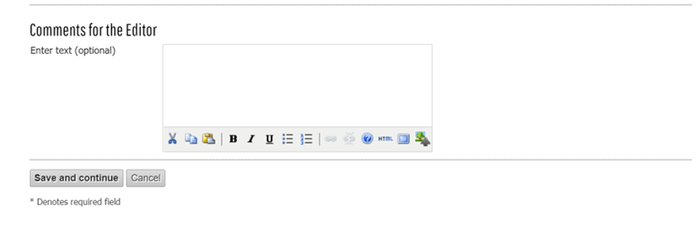 
6. Setelah mengisi komentar, silahkan klik tombol Save and Continue, maka akan muncul tampilan berikut Pada bagian ini juga banyak ditemukan kesalahan yang dilakukan oleh author yang menyebabkan naskahnya tidak dapat di proses atau bahkan diabaikan oleh editor. Kesalahan yang banyak dilakukan adalah penulis memilih file yang akan di upload, lalu klik save and continue. Langkah seperti ini menyebabkan file tidak terupload, sehingga naskah tidak mungkin di proses oleh editor jurnal. Lalu apa yang harus dilakukan? Silahkan pilih file yang akan disubmit pada bagian Choose File. Setelah itu, pastikan untuk klik tombol UPLOAD pada bagian kanan sampai muncul file terupload seperti gambar berikut: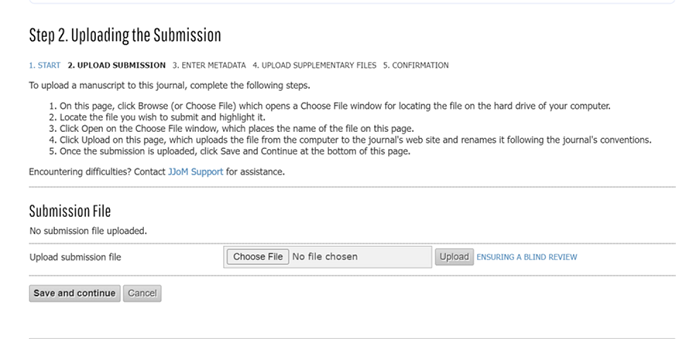 Jika sudah muncul nama file seperti ini, artinya naskah sudah terupload dengan benar. Silahkan klik Save and Continue.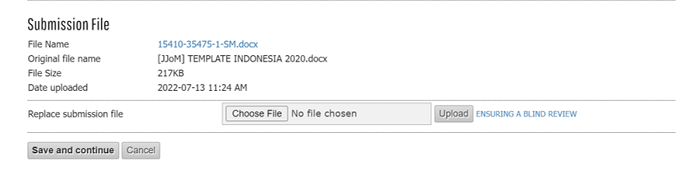
7. Pada bagian selanjutnya, author akan masuk pada bagian metadata yang memuat isian informasi tentang penulis, judul, abstrak, kata kunci, dan referensi. Pada tahap ini akan langsung muncul tampilan dengan nama author yang melakukan submisi naskah seperti gambar berikut: Kesalahan yang sering dilakukan penulis pada bagian ini adalah melewatkan untuk menginput nama penulis kedua, ketiga, dst. Langkah yang benar, harusnya dilengkapi semua data penulis dengan cara klik Add Author, lengkapi semua identitas seperti nama lengkap, afiliasi, email, country. Jika author sudah lengkap, silahkan isi Judul Naskah, Abstrak (disarankan abstrak berbahasa inggris), kata kunci, lalu daftar referensi. Setelah itu klik save and continue.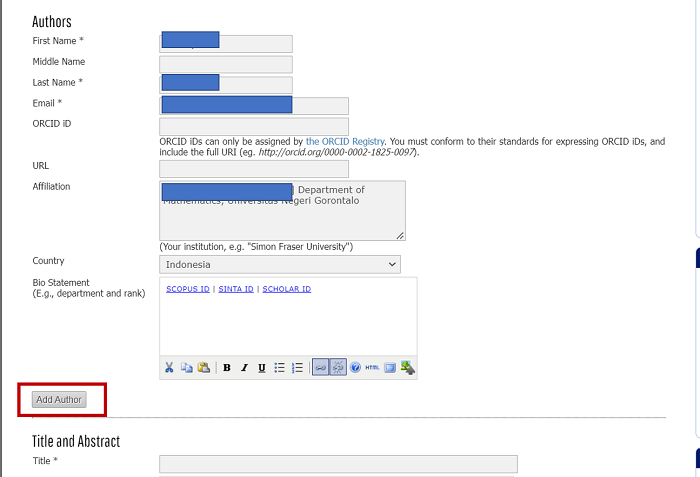
8. Selanjutnya proses akan masuk pada bagian supplementary file. Bagian ini sifatnya optional, tapi author dapat menambahkan file tambahan yang kemungkinan diperlukan oleh editor atau reviewer seperti Hasil Cek Plagiat, Data, atau file tambahan lainnya. Upload file dilakukan dengan cara yang sama pada tahap 2. Jika tidak ada file atau file selesai diupload silahkan klik save and continue.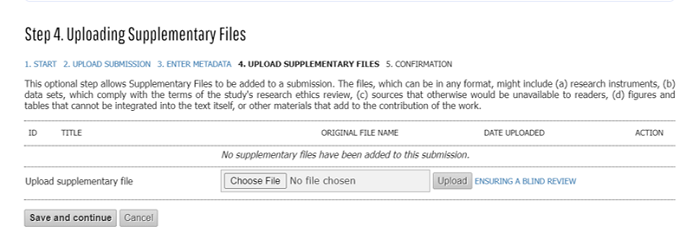
9. Langkah terakhir adalah langkah konfirmasi. Silahkan klik Finish Submission, maka muncul tampilan berikut yang artinya proses penyerahan naskah telah selesai.
10. Silahkan klik Active Submission untuk melihat status naskah yang telah diserahkan. Disarankan untuk melihat status naskah secara berkala melalui akun author atau informasi yang sewaktu-waktu dapat dikirim oleh editor melalui email. Keterlambatan author dalam merespon editor bisa jadi salah satu penyebab naskah tidak dapat diterbitkan.

Demikian turorial Penyerahan Naskah pada Jurnal Ilmiah berbasis OJS 2. Semoga bermanfaat. Berikut, kami mengundang anda untuk menerbitkan naskah dengan kualitas terbaik sesuai dengan scope beberapa jurnal kami berikut:

• Jambura Journal of Mathematics
• Jambura Journal of Biomathematics
• Jambura Journal of Mathematics Education
• Jambura Journal of Probability and Statistics
• Euler: Jurnal Ilmiah Matematika, Sains, dan Teknologi