Transmisi Coronavirus Disease (COVID-19) dalam Representasi Pemodelan Matematika
Pemodelan matematika merupakan salah satu alat utama dalam perencanaan epidemik yang dapat membantu mempermudah penyelesaian masalah dalam kehidupan nyata, termasuk masalah pandemik COVID-19. Pemodelan matematika dapat membantu memahami dan mengidentifikasi hubungan penyebaran COVID-19 dengan berbagai parameter epidemiologi, membantu dalam perencanaan masa depan dan mempertimbangkan langkah-langkah pengendalian yang tepat.
Dalam tulisan ini dikembangkan sebuah model matematika transmisi Coronavirus Disease (COVID-19). Model dirancang dengan mempertimbangkan faktor-faktor epidemiologi pada penyebaran COVID-19, termasuk dengan mempertimbangkan kondisi real dari kasus yang terjadi hingga ditetapkannya kasus ini sebagai kasus pandemik.
Model yang dirancang pada bagian ini fokus pada pola penyebaran virus diantara manusia setelah virus ini mewabah. Kami tidak lagi mengkaji bagaimana virus ini menjangkiti manusia pada awal kasus, melainkan bagaimana virus ini menyebar melalui interaksi yang terjadi antar sesama manusia. Selain itu, individu terpapar yang masih dalam masa inkubasi, diasumsikan dapat menularkan virus secara tidak sadar jika berinteraksi dengan manusia rentan. Hal ini perlu dipertimbangkan karena diduga penyebaran kasus banyak terjadi melalui individu terpapar karena tidak adanya gejala yang terdeteksi. Lebih lanjut, pada model ini dipertimbangkan parameter yang mewakili kasus kematian yang disebabkan karena virus, melihat realita banyaknya kasus kematian karena COVID-19. Kasus kematian diasumsikan terjadi pada kelompok individu terinfeksi dengan gejala klinis. Adanya karantina terhadap individu yang terpapar atau lebih umum dikenal dengan ODP (Orang Dalam Pemantauan) juga dipertimbangkan pada model ini.
Total populasi manusia dinotasikan dengan N(t) dibagi menjadi enam kelas, yaitu manusia rentan S(t), manusia terpapar dalam masa inkubasi E(t), manusia terinfeksi tanpa gejala klinis A(t), manusia terinfeksi disertai gejala klinis I(t), manusia yang dikarantina Q(t) dan manusia yang pulih dari COVID-19 R(t). Dengan demikian, total populasi dinyatakan dengan N(t)=S(t)+E(t)+A(t)+I(t)+Q(t)+R(t).
Laju rekrutmen kelahiran dan tingkat kematian alami manusia masing-masing diberikan oleh parameter Π dan μ. Manusia rentan (S) akan terinfeksi melalui kontak yang cukup dengan individu rentan (E), individu terinfeksi dengan gejala klinis (I) maupun dengan individu terinfeksi tanpa gejala klinis (A), masing-masing sebesar ηζseSE, ηζsiSI, dan ηζsaSA dimana η adalah peluang infeksi saat terjadi kontak antar individu. ζse, ζsi, dan ζsa masing-masing menyatakan laju kontak antara individu rentan (S) kelompok individu E, I, dan A. Parameter θ dan σ, masing-masing adalah proporsi individu yang terinfeksi tanpa gejala klinis proporsi individu terpapar yang dikarantina, sementara parameter α menyatakan laju perpindahan individu terpapar ke individu yang dikarantina. Parameter ω dan ϖ masing-masing merepresentasikan tingkat transmisi setelah menyelesaikan masa inkubasi dan berpindah ke kelas I dan A. Individu yang dikarantina dapat berpindah ke kelas individu terinfeksi yang disertai gejala klinis dengan laju ?, dengan proporsi individu sebesar φ. Paramater τ,β,ρ masing-masing menyatakan tingkat pemulihan individu terinfeksi tanpa gejala klinis, individu dikarantina, dan individu terinfeksi disertai gejala klinis dan berpindah ke kelas individu yang telah pulih. Selanjutnya, tingkat kematian yang disebabkan oleh virus COVID-19 pada kelas I direpresentasikan dengan δ.
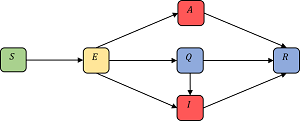
"Gambar1. Diagram skematis transmisi COVID-19"
Gambar 1 menunjukkan pola transimi COVID-19 dengan model berikut,
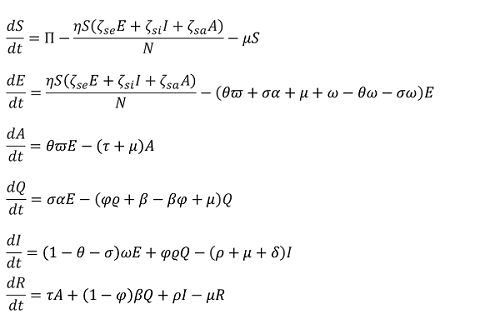
Dari model ini dapat dikonstruksi bilangan reproduksi dasar yang digunakan sebagai tolak ukur penularan penyakit dalam suatu populasi. Dalam hal ini, diperoleh formulasi bilangan reproduksi dasar berikut,
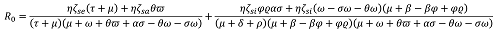
Selanjutnya, penting untuk dilakukan analisis terhadap parameter yang terlibat untuk mengetahui tingkat sensitivitas parameter terhadap laju penularan penyakit. Indeks sensitivitas normalisasi dari R0 yang terdiferensialkan pada parameter p diberikan oleh,
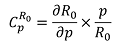
Parameter dengan indeks sensitivitas positif menunjukkan adanya kontrubusi positif pada peningkatan bilangan reproduksi dasar, artinya jika nilai parameter ini diperbesar, maka akan berkontribusi pada peningkatan bilangan reproduksi dasar. Sementara parameter dengan indeks sensitivitas negatif menunjukkan adanya kontrubusi negatif pada peningkatan bilangan reproduksi dasar, artinya jika nilai parameter ini diperbesar, maka akan berkontribusi pada penurunan bilangan reproduksi dasar. Untuk mengidentifikasi Indeks Sensitivitas, kami gunakan nilai-nilai parameter bedasarkan hasil fitting berdasarkan data real kasus COVID-19 dari berbagai referensi terpercaya yang telah dipublikasikan.
Indeks sensitivitas menunjukan bahwa interaksi dengan individu terpapar dan peluang terjadinya transmisi saat kontak yang paling dominan berkontribusi pada penularan COVID-19, sementara proporsi banyaknya individu terpapar yang dikarantina menjadi yang paling dominan menekan laju penularan COVID-19. Tindakan yang perlu dilakukan adalah menekan laju interaksi dengan individu terpapar dan memaksimalkan karantina pada individu yang terdeteksi atau diduga telah terpapar. Permasalahan yang dihadapi untuk memaksimalkan tindakan ini adalah minimnya pengetahuan atau alat yang dapat mendeteksi orang-orang yang telah terpapar oleh COVID-19, artinya kita tidak dapat mengetahui dengan pasti, siapa yang telah terpapar dan siapa yang masih bersih dari COVID-19. Dengan demikian, upaya-upaya preventif seperti social distancing dan Physical Distancing hingga saat ini masih menjadi satu-satunya cara efektif untuk menghentikkan laju penyebaran COVID-19.
[DAC63053] Pemodelan Matematika 2019
Berikut slide beberapa materi yang berkaitan dengan mata kuliah Pemodelan Matematika. Klik judul untuk mendownload materi.
A. Referensi
- Principles of mathematical modeling
- An Introduction to Mathematical Modelling
- Model SIR Penyebaran Penyakit
- Referensi Publikasi
B. Slide Ajar
- Konsep Dasar Pemodelan dan Klasifikasi Model
- Model Pertumbuhan Populasi
- Model Deterministik Dinamika Populasi
- Model Deterministik Penyebaran Penyakit
C. Informasi Tugas Mata Kuliah
- Template Pelaporan Tugas Akhir Mahasiswa
- Template Artikel menyesuaikan dengan Template pada Jambura Journal of Mathematics
- Tips Menulis Artikel Dapat Diakses DISINI
Catatan:
- Slide ini hanya bersifat ringkasan, sehingga mahasiswa dianjurkan untuk tetap menggunakan referensi lain yang lebih lengkap untuk pemahaman topik pemodelan matematika dengan baik.
- Informasi lainnya akan diupdate kemudian.
Model SIR untuk Penyebaran Penyakit
Author(s): David Smith and Lang Moore
Artikel ini dapat digunakan sebagai salah satu referensi pada mata kuliah Pemodelan Matematika. Ikuti tautan berikut untuk pembaahasan selengkapnya.
- Model SIR untuk Penyebaran Penyakit - Latar Belakang
- Model SIR untuk Penyebaran Penyakit - Model Persamaan Diferensial
- Model SIR untuk Penyebaran Penyakit - Metode Euler
- Model SIR untuk Penyebaran Penyakit - Hubungan Parameter dengan Data
- Model SIR untuk Penyebaran Penyakit - Jumlah Kontak
- Model SIR untuk Penyebaran Penyakit - Kekebalan
- Model SIR untuk Penyebaran Penyakit - Ringkasan
Model SIR untuk Penyebaran Penyakit - Ringkasan
Author(s): David Smith and Lang Moore Kembali
- Explain briefly the modeling steps that lead to the SIR model.
- Given a population and disease combination for which the SIR model is appropriate, what are the possible outcomes when a trace of infection is introduced into the population? How can you tell whether there will be an epidemic?
- Does "epidemic" mean that almost everyone will get the disease? If so, what keeps the spread of disease going? If not, what causes the epidemic to end before everyone gets sick?
- How can it happen that a large percentage of a population may get sick during an epidemic even though only a small percentage is sick at any one time?
- Explain briefly the key idea for finding solutions of an SIR model without finding explicit solution formulas.
- Describe briefly the meaning and significance of contact number.
- Describe briefly the meaning and significance of herd immunity. How can an inoculation program lead to herd immunity?
- The contact number for poliomyelitis in the U.S. in 1955 was 4.9. Explain why we have been able to eradicate this disease even though we cannot eradicate measles. Give a careful argument -- "smaller contact number" is an observation, not an explanation.
Link Artikel
- Model SIR untuk Penyebaran Penyakit - Latar Belakang
- Model SIR untuk Penyebaran Penyakit - Model Persamaan Diferensial
- Model SIR untuk Penyebaran Penyakit - Metode Euler
- Model SIR untuk Penyebaran Penyakit - Hubungan Parameter dengan Data
- Model SIR untuk Penyebaran Penyakit - Jumlah Kontak
- Model SIR untuk Penyebaran Penyakit - Kekebalan
- Model SIR untuk Penyebaran Penyakit - Ringkasan
Model SIR untuk Penyebaran Penyakit - Kekebalan
Author(s): David Smith and Lang Moore Kembali
Setiap strain flu memberi kekebalan di masa yang akan datang bagi pengidapnya. Untuk penyakit seperti ini, jika hampir semua orang mengalaminya, maka mereka yang belum mengalami akan terlindung dari darinya sehingga tidak cukup suseptibilitas tersisa di populasi untuk memungkinkan epidemi terjadi. Perlindungan seperti ini disebut kekebalan kelompok.
Pada Bagian 3 kita bereksperimen dengan ukuran relatif pada b dan k, dan kita temukan bahwa, jika b lebih kecil dari k, maka tidak ada epidemi yang dapat berkembang. Kemudian pada Bagian 4, jika jumlah kontak c = b/k cukup kecil, maka tidak akan ada kasus epidemi. Namun cara lain untuk mencegah terjadinya epidemi adalah dengan mengurangi populasi pada individu rentan secara artifisial dengan inokulasi.
Inti dari inokulasi adalah menciptakan kekebalan kelompok dengan merangsang antibody sebanyak mungkin yang dapat memberikan kekebalan. Dengan demikian inokulasi menciptakan jalur langsung dari kelompok individu rentan ke kelompok individu yang pulih tanpa melewati kelompok terinfeksi (lihat diagram di bawah). Dan program inokulasi berskala besar untuk mencegah epidemi yang akan datang cukup cepat untuk menurunkan populasi rentan ke tingkat yang aman sehingga jika tingkat infeksi masuk ke populasi, beberapa orang mungkin sakit, namun tidak ada epidemi yang akan berkembang.
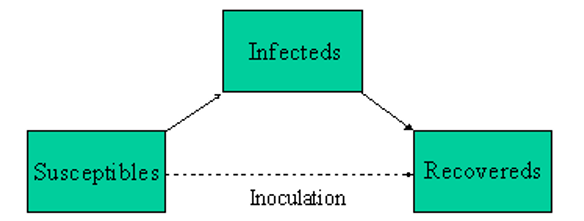
Jadi, berapa proporsi penduduk yang harus diinokulasi untuk mendapatkan kekebalan kelompok? Atau, dengan kata lain, seberapa kecil s0 yang harus dipenuhi untuk memastikan bahwa epidemi tidak dapat dimulai? Itu tergantung pada jumlah kontak.
1. Mengontrol terjadinya kasus epidemi sama dengan menjaga di/dt tetap negatif dari t = 0 dan seterusnya, mengapa demikian?
2. Tulis ruas kanan dari persamaan diferensial proporsi individu terinfeksi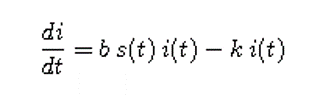
Jelaskan mengapa salah satu faktor selalu positif dan mengapa tanda faktor lain tergantung pada s (t)?
3. Jelaskan mengapa s(t) merupakan fungsi turun, sehingga memiliki nilai terbesar pada t=0. Hal ini berakibat, jika di/dt negatif pada waktu 0, maka ia tetap negatif.
4. Tunjukkan bahwa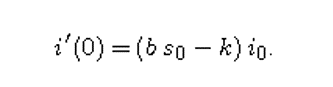
Jelaskan mengapa, jika s0 kurang dari 1/c, maka tidak ada epidemi yang bisa berkembang.
5. Dari tahun 1912 hingga 1928, jumlah kontak untuk kasus campak di AS adalah 12,8. Jika kita berasumsi bahwa c masih 12,8 dan inokulasi 100% efektif (setiap orang yang diinokulasi memperoleh kekebalan dari penyakit), berapa proporsi populasi yang harus diinokulasi untuk mencegah epidemi?
6. Anggaplah vaksin hanya 95% efektif. Berapa proporsi penduduk harus diinokulasi untuk mencegah epidemi campak?
Link Artikel
- Model SIR untuk Penyebaran Penyakit - Latar Belakang
- Model SIR untuk Penyebaran Penyakit - Model Persamaan Diferensial
- Model SIR untuk Penyebaran Penyakit - Metode Euler
- Model SIR untuk Penyebaran Penyakit - Hubungan Parameter dengan Data
- Model SIR untuk Penyebaran Penyakit - Jumlah Kontak
- Model SIR untuk Penyebaran Penyakit - Kekebalan
- Model SIR untuk Penyebaran Penyakit - Ringkasan
Kategori
Arsip
- July 2023 (3)
- January 2023 (1)
- December 2022 (1)
- August 2022 (1)
- July 2022 (6)
- March 2022 (1)
- September 2021 (2)
- October 2020 (1)
- July 2020 (2)
- April 2020 (1)
- November 2019 (1)
- September 2019 (1)
- August 2019 (2)
- July 2019 (1)
- May 2019 (1)
- February 2019 (1)
- September 2018 (2)
- August 2018 (1)
- July 2018 (4)
- June 2018 (5)
- September 2017 (2)
- August 2017 (1)
- April 2017 (1)
- October 2016 (1)
- September 2016 (2)
- September 2015 (4)
- June 2015 (1)
Blogroll
- 01 Sistem Informasi Akademik
- 02 Repository UNG
- 03 Universitas Negeri Gorontalo
- 04 Beasiswa DIKTI
- 05 Beasiswa LPDP
- 06 BookFi
- 07 Indonesian Mathematical Society
- 08 EBSCOhost
- 09 Library Genesis
- 10 Khan Academy
- 11 Blog Pribadi
- 12 Twitter
- 13 Facebook
- 14 Pdf Drive
- 15 Pangkalan Data UNG
- 16 Differential Equation
- 17 Math is Fun
- 18 Jambura Journal of Mathematics
- 19 OSF
- 20 Sci-Hub
- 21 Researchsquare
- 22 Kalkulator Math
- 23 Gometa
- 24 Microsite
- 25 Wordwall
- 26 Science Direct
- 27 BSRE BSSN
- 28 OpenAI
- 29 Quillbot
- 30 Perplexity
- 31 Citation FInder
