Model SIR untuk Penyebaran Penyakit - Metode Euler untuk Sistem

26 June 2018 14:36:37 Dibaca : 2158

Author(s): David Smith and Lang Moore Kembali

Pada bagian, kita akan menampilkan solusi dari model SIR melalui pendekatan solusi numerik, seperti Metode Euler yang sudah biasa kita gunakan. Namun demikian, kita tetap meninjau kembali gagasan dasar dari metode ini.

Ingat kembali gagasan Metode Euler bahwa:

"Jika kita memiliki rumus slope/kemiringan," yaitu, cara untuk menghitung dy/dt pada sembarang titik (t, y), maka kita dapat menghasilkan barisan pada nilai y,

y0, y1, y2, y3, ...

dengan dimulai dari y0 yang diberikan dan menghitung setiap kenaikan sebagai kemiringan (slope). Artinya,

y_n = y_n-1 + slope_n-1*Delta_t

di mana Delta_t adalah ukuran langkah kecil yang sesuai dalam domain waktu.

Tidak jadi masalah dalam perhitungan ini jika rumus kemiringan yang terjadi tergantung tidak hanya pada variabel t dan y tetapi juga pada variabel lain. Katakanlah x dan z, selama kita tahu bagaimana hubungan x dan z dengan t dan y. Jika x dan z terjadi sebagai variabel dependen lain dalam sistem persamaan diferensial, maka kita dapat menghasilkan nilai x dan z dengan cara yang sama.

Tentu saja, untuk model SIR, kita ingin nama variabel dependen lainnya menjadi s, i, dan r. Dengan demikian kita memiliki tiga rumus Euler dalam bentuk

Untuk lebih jelas, kita ingat kembali model SIR,

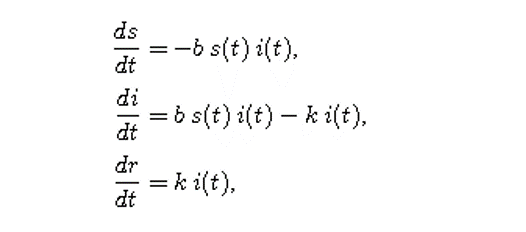
dalam formula Euler dapat dikonversi menjadi,

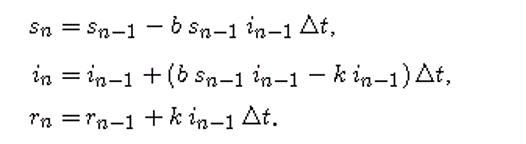
Tentu saja, untuk menghitung sesuatu dari rumus ini, kita harus memiliki nilai eksplisit untuk b, k, s(0), i(0), r(0), dan Delta_t. Pada bagian ini kami mengeksplorasi kecukupan formula ini untuk menghasilkan solusi dari model SIR. Jika ada aplikasi yang memiliki Metode Euler sebagai pilihan, kita boleh menggunakannya daripada harus mengonstruksi rumus dari awal.

Pada lembar kerja aplikasi yang anda gunakan, terdapat perintah untuk menemukan solusi persamaan diferensial. Gunakan perintah ini, dengan nilai sampel b = 1/2 dan k = 1/3, untuk menghasilkan solusi grafis dari persamaan SIR, mulai dari s(0) = 1, i(0) = 1.27e-6, dan r(0) = 0.
Sekarang bangkitkan solusi Metode Euler untuk tiga sektor populasi. Mulai dengan ukuran langkah yang relatif kasar Delta_t = 10 hari, dan biarkan rentang t hingga 150 hari. Sesuaikan solusi ini pada solusi "exact" Langkah 1. Menurut anda, apakah Metode Euler dapat digunakan untuk memprediksi solusi yang tepat dari sistem? Mengapa atau mengapa tidak? Apa karakteristik Metode Euler yang menyebabkan prediksi solusi berperilaku seperti itu?
Ubah ukuran langkah menjadi 1 hari dan plot kembali solusi Metode Euler. Sekarang apakah hal ini dapat memprediksi solusi yang tepat dari sistem? Mengapa atau mengapa tidak?
Temukan ukuran langkah yang tepat pada Metode Euler untuk memprediksi solusi yang tepat dari sistem.

Link Artikel

Pemodelan Matematika 1 Komentar

Model SIR untuk Penyebaran Penyakit - Model Persamaan Diferensial

17 June 2018 19:13:47 Dibaca : 5930

Author(s): David Smith and Lang Moore Kembali

Sebagai langkah pertama dalam proses pemodelan, kita mengidentifikasi variabel independen dan dependen. Variabel independen adalah waktu t, yang diukur dalam beberapa hari. Kita pertimbangkan dua kelompok variabel dependen yang berkaitan.

Kelompok variabel dependen pertama mewakili setiap kelompok populasi manusia, masing-masing dalam fungsi waktu yaitu:

S = S(t) mewakili proporsi individu rentan,

I = I(t) mewakili proporsi individu terinfeksi dan

R = R(t) mewakili proporsi individu yang pulih dari penyakit.

Kelompok variabel dependen selanjutnya mewakili hasil perbandingan dari masing-masing kategori populaasi dengan total populasi. Dengan demikian, jika N adalah total populasi (Misal: 7.900.000), maka diperoleh

s(t) = S(t)/N mewakili banyaknya individu rentan,

i(t) = I(t)/N mewakili banyaknya individu terinfeksi dan

r(t) = R(t)/N mewakili banyaknya individu yang pulih dari penyakit.

Mungkin akan terlihat lebih alami untuk bekerja dengan jumlah populasi, namun beberapa perhitungan akan lebih sederhana jika digunakan nilai proporsi sebagai gantinya. Dua kelompok variabel dependen diatas saling proporsional satu sama lain, sehingga salah satu akan kita gunakan untuk memperoleh informasi terkait perkembangan penyakit.

Selanjutnya kita buat beberapa asumsi terkait tingkat perubahan variabel antara lain:

Tidak ada penambahan pada ke kelompok rentan, karena kita mengabaikan kelahiran dan imigrasi. Satu-satunya cara individu meninggalkan kelompok rentan adalah dengan berpindah ke kelompok terinfeksi.
Kita berasumsi bahwa laju perubahan S(t), tergantung pada jumlah individu rentan, jumlah individu terinfeksi, dan jumlah kontak antara individu rentan dengan individu terinfeksi.
Lebih kuhusus, kita berasumsi bahwa setiap individu yang terinfeksi memiliki jumlah kontak tetap b, per hari yang cukup untuk menyebarkan penyakit. Tidak semua kontak terjadi dengan individu rentan.
Jika kita berasumsi bahwa populasi bercampur secara homogen, maka proporsi kontak dengan individu rentan adalah s(t). Dengan demikian, rata-rata setiap individu yang terinfeksi menghasilkan b*s(t) individu terinfeksi baru per hari. [Dengan populasi rentan yang besar dan populasi terinfeksi yang relatif kecil, kita dapat mengabaikan situasi penghitungan yang rumit seperti individu rentan bertemu lebih dari satu individu terinfeksi pada hari tertentu].
Kita juga berasumsi bahwa ada proporsi tetap k dari kelompok individu terinfeksi yang akan pulih setiap hari tertentu. Misalnya, jika durasi rata-rata infeksi adalah tiga hari, maka rata-rata sepertiga dari populasi yang terinfeksi saat ini akan pulih pulih setiap harinya. (Untuk lebih jelasnya, yang kita maksud dengan "individu terinfeksi" adalah individu yang benar-benar "menular," yaitu individu yang mampu menyebarkan penyakit ke individu rentan. Individu yang telah "pulih" masih mungkin merasakan gejala penyakit, dan bahkan bisajadi meninggal dunia kemudian akibat pneumonia).

Berdasarkan asumsi-asumsi ini, kita lihat apa yang dapat diketahui tentang turunan dari variabel dependen kita.

Perhatikan dan ikuti langkah-langkah berikut ini. Anda dipersilahkan untuk menjawab beberapa pertanyaan yang diberikan:

1. Berdasarkan asumsi yang telah dibuat, bagaimana menurut Anda prilaku s(t), i(t) dan r(t) terhadap waktu?

2. Buat sketsa grafik fungsi tersebut masing-masing pada selembar kertas berdasarkan pemahaman anda.

3. Jelaskan mengapa, pada setiap waktu t, s (t) + i (t) + r (t) = 1.

4. Persamaan untuk Individu Rentan

Jelaskan dengan seksama setiap komponen dari persamaan diferensial berikut:

mengikuti penjelasan yang telah diberikan sebelumnya. Khususnya:

Mengapa terdapat faktor I(t) pada persamaan?
Dari mana asal tanda negatif pada persamaan tersebut?

Selanjutnya jelaskan bagaimana persamaan ini dikonversi ke persamaan diferensial berikut untuk s(t).

5. Persamaan untuk Individu yang telah Pulih

Jelaskan bagaimana menemukan persamaan diferensial untuk r(t),

mengikuti dari Langkah yang telah dilakukan pada nomor 4.

6. Persamaan untuk Individu Terinfeksi

Jelaskan kenapa diperoleh

Asumsi apa yang mencerminkan model ini?

Selanjutnya, jelaskan dengan seksama bagaimana komponen dari persamaan

mengikuti langkah-langkah yang telah Anda lakukan sejauh ini. Khususnya,

Mengapa terdapat dua suku pada persamaan?
Mengapa laju perpindahan individu dari populasi terinfeksi ke populasi pulih harus bergantung hanya pada i(t)?
Dari mana tanda asal minus pada persamaan?

Akhirnya, kita dapat menyelesaikan model ini dengan memberikan nilai awal pada masing-masing persamaan diferensial. Untuk virus ini "flu Hong Kong di New York City pada akhir tahun 1960", hampir tidak ada yang kebal pada awal-awal peyebaran penyakit, sehingga hampir semua orang rentan terhadap penyakit. Kita asumsikan bahwa ada tingkat infeksi dalam populasi, katakanlah, 10 orang. Dengan demikian, nilai awal kita yang berikan untuk variabel populasi adalah

S(0) = 7,900,000

I(0) = 10

R(0) = 0

Dalam bentuk variabel berskala, kondisi awal ini sama dengan

s(0) = 1

i(0) = 1.27 x 10- 6

r(0) = 0

(Catatan: Jumlah populasi awal kita tidak sepenuhnya tepat N, demikian juga dengan nilai proporsinya tidak sepenuhnya tepat tepat 1. Namun Tingkat infeksi yang sangat kecil sehingga hal ini tidak akan berpengaruh pada hasil).

Model lengkap yang diperoleh adalah

Kita belum mengetahui nilai untuk parameter b dan k, namun kita dapat memberi nilai estimasi sesuai kebutuhan agar sesuai dengan data kematian. Kita sudah memperkirakan rata-rata masa penularan dalam jangka waktu tiga hari, sehingga digunakan k = 1/3. Jika diperkirakan bahwa setiap terinfeksi akan membuat kontak yang mungkin menginfeksi setiap dua hari, maka b dapat diamusikan 1/2. Kita tegaskan kembali bahwa ini nilai hanyalah prediksi. Plot berikut menunjukkan kurva solusi untuk nilai b dan k tersebut.

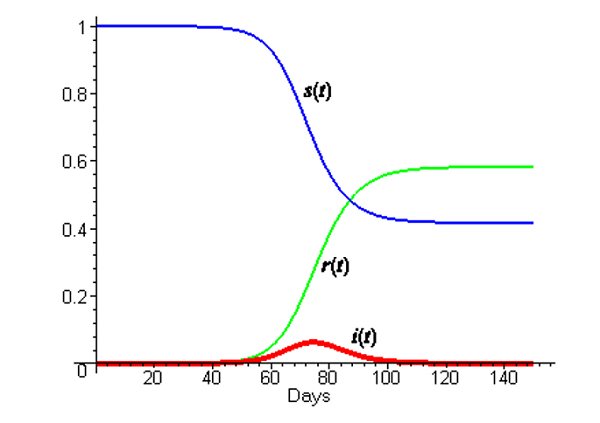
7. Bandingkan jawaban anda pada langkah 1 dan 2 dengan plot di atas. Bagaimana ide-ide itu dibandingkan dengan gambar di atas?

Bagaimana pendapat Anda tentang tingkat infeksi yang relatif rendah pada puncak epidemi?
Dapatkah menjelaskan bagaimana tingkat infeksi yang rendah dapat menyebabkan lebih dari separuh penduduk jatuh sakit?

Pada Bagian selanjutnya, kita akan melihat bagaimana kurva solusi dapat dihitung bahkan tanpa rumus untuk fungsi solusi.

Link Artikel

Pemodelan Matematika 1 Komentar

Model SIR untuk Penyebaran Penyakit - Latar Belakang

17 June 2018 08:47:51 Dibaca : 1203

Author(s): David Smith and Lang Moore Kembali

Selama musim dingin 1968-1969, Amerika Serikat diserang oleh strain baru influenza yang ganas, yang disebut flu Hong Kong. Pada saat itu, tidak ada vaksin flu yang tersedia, sehingga lebih banyak orang yang terinfeksi. Kita akan mempelajari penyebaran penyakit ini melalui satu populasi yaitu penduduk di Kota New York. Data yang ditampilkan dalam tabel berikut adalah jumlah kematian pekanan akibat "pneumonia-influenza".

(Sumber: Centers for Disease Control. Click here for a recent CDC view of influenza pandemics.)

Pekan	Angka Kematian	Pekan	Angka Kematian
1	14	8	108
2	28	9	68
3	50	10	77
4	66	11	33
5	156	12	65
6	190	13	24
7	156

Grafik menampilkan data yang sama.

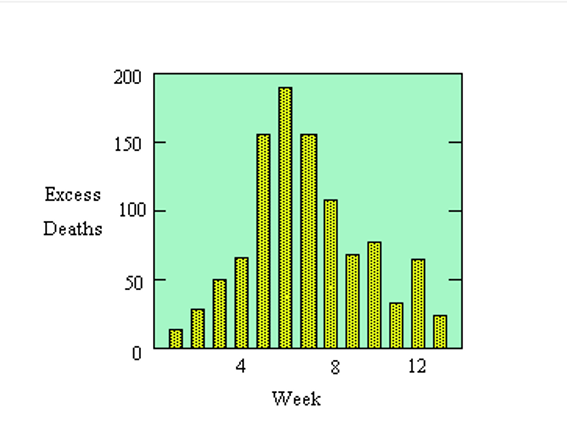
Relatif sedikit penderita flu yang meninggal karena penyakit atau komplikasinya, bahkan tanpa vaksin. Namun, kita mungkin berasumsi bahwa proporsi jumlah kematian dalam seminggu terakhir lebih besar dibandingkan dengan jumlah kasus baru flu pada beberapa minggu sebelumnya, katakanlah, tiga minggu sebelumnya. Dengan demikian angka-angka dalam tabel mencerminkan (secara proporsional) adanya kenaikan dan penurunan dalam jumlah kasus baru flu Hong Kong. Kita akan memodelkan penyebaran penyakit semacam itu sehingga kita dapat memprediksi kemungkinan adanya kasus epidemi serupa di masa yang akan datang.

Pada waktu tertentu selama wabah flu terjadi, kita ingin mengetahui jumlah orang yang terinfeksi. Kita juga ingin tahu jumlah yang telah terinfeksi dan telah pulih, karena orang-orang ini sekarang memiliki kekebalan terhadap penyakit. Sisa populasi masih rentan terhadap penyakit. (Kita berasumsi bahwa populasi yang sama berada di New York selama minggu-minggu terjadinya kasus epidemi).

Dengan demikian, setiap saat, populasi total tetap (sekitar 7.900.000 dalam kasus Kota New York pada akhir 1960-an) dapat dibagi menjadi tiga kelompok yang berbeda: